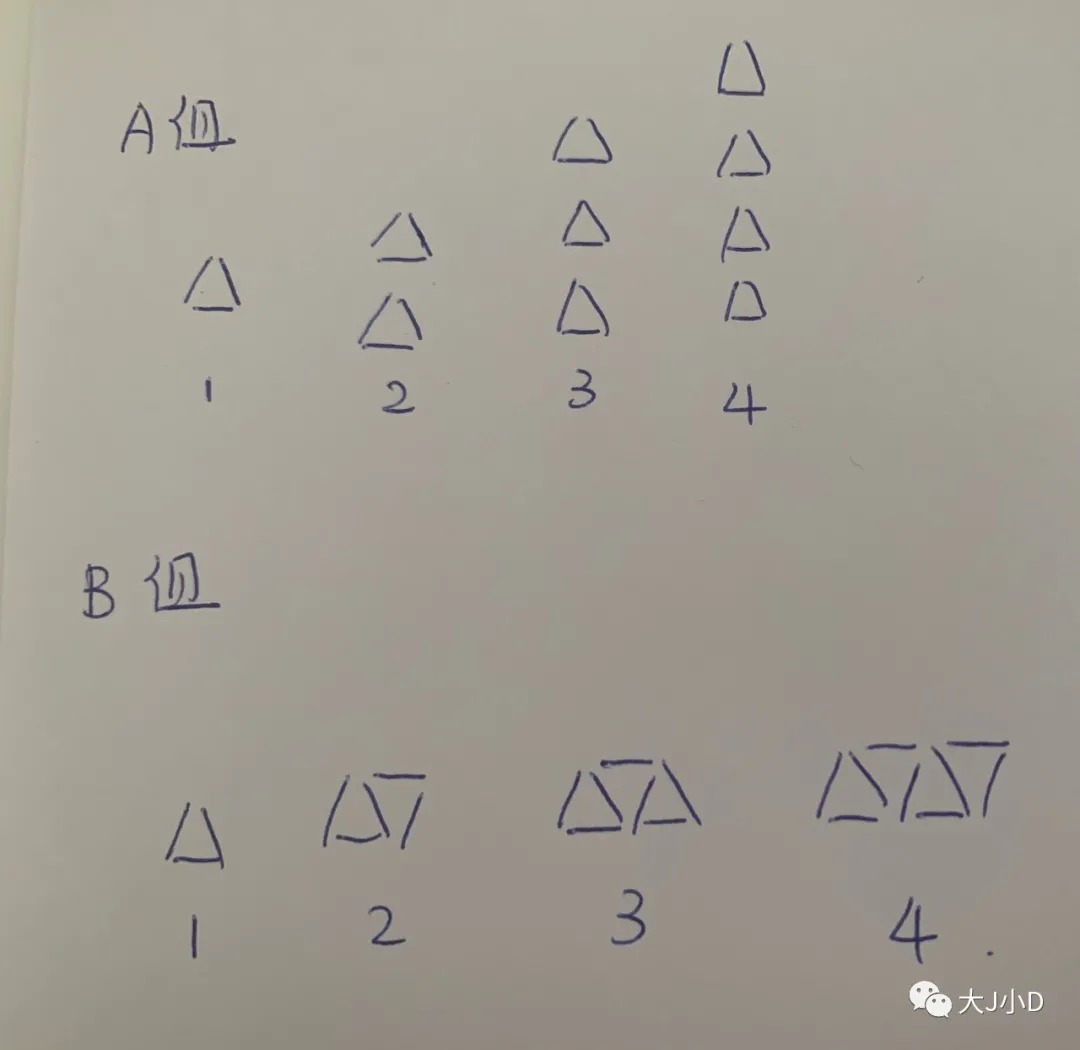
今天分享之前，先来给大家出一个题目。下面两组规律，能否分别写出n序列的代数表达式。

估计对大部分朋友来说都不难吧，第一组答案是3n，第二组答案是2n+1。

但如果我告诉你，这是我们邻居6岁半孩子的题目，你是不是会和我一样非常惊讶呢？

大家应该听说过，纽约曼哈顿有个G&T项目（天才儿童班），这个孩子就考进去了。

下面要分享的并不是想引起大家对于“别人家孩子”的焦虑，我女儿小D也无法完成这个题目。

当我询问那个小孩，她是怎么得出这个答案的。

她的思考过程非常有意义，而这恰恰就是我们每个父母都可以借鉴的数学启蒙的思路。

她当时拿出了一些小积木棍，搭出下面的形状，和我说，“这是找规律，你看下面这些图形就符合数字，我们只要思考这样的图形后面的规律是什么？”

我又问她，你是怎么想到用图形来帮助你思考的？

她告诉我，这些就是我们平时玩的啊，大家会自己搭一些图形规律，然后同学和老师一起观察，推测规律是什么？

规律，如果你已经开始了早期数学启蒙，恐怕不会陌生。这就是数学思维的五大能力之一，

数学五大能力，对应的分别是数数、空间、等式、规律和测量。

规律看着很简单，也很容易被忽视。如果不是邻居小女孩的这道题目，我想大家都无法把规律和数学联系在一起的吧。

那今天就好好来讲一讲。

什么是规律？

规律，顾名思义，就是一个序列按照一定规则不断重复出现。对于学龄前孩子来说，最基本的就是下面这三个能力。

1、理解

第一步是根据实物进行，最简单的就是ABAB规律。比如“红黄红黄红黄”。一开始孩子只要认出这是规律就好了。

随后是复杂规律，比如AABAAB、ABAABA，类似这样的，同样也可以按照上面的进行。

用实物也可以

2、预测

然后可以预测规律，比如给了“红黄红黄”，可以知道接下来也是“红黄”。

3、创造

最后就是自己可以创造新序列，比如“葡萄苹果葡萄苹果”。

延展是关键

看到这里，肯定很多朋友就急了，这些我孩子都会啊，那怎么可以完成开头这样的解题呢？

其实就是这样的“着急”，恰恰到后来拉开了差距。

好的数学启蒙，每次引入新的概念时，即使孩子一下子就掌握了这个概念，向前推进的速度也要放慢。

这是我今天最想和大家强调的一点，我们经常容易为了完成某个目标，而着急往前赶孩子。

结果很多内容，看上去孩子“会”了，其实是一知半解，甚至只是死记硬背、表演性质的。

开头的这个解题能力，其实就是关于规律的延展能力。

我们总觉得这是数学启蒙，就会立马想到延展到数字规律，这反而是拔苗助长了。

一般孩子3、4岁的时候引入规律后，就需要跨界延展。

不仅仅是颜色，不仅仅是物体，还可以是语言，也可以是动作，最后才是数字。

当一个孩子可以自发地把自己学到的内容和生活结合起来，这就说明他们真正掌握了，那么之后的学科知识就是水到渠成。

动作规律

这是很多音乐早教课经常用的，就是大家接龙进行动作拷贝，完全可以在家做。

1、动作接龙

和孩子面对面，我们先挥舞左手、挥舞右手、摸摸鼻子，然后孩子模仿我们的动作一遍，轮到我们再重复一遍，这样就是规律在生活中的展示。

2、拍手游戏

我们小时候玩的“你拍一，我拍一”这类的拍手游戏，其实就是动作规律。大家也能多和孩子玩。

文字规律

现在很多绘本其实都会包含文字规律，亲子阅读的时候不妨做个有心人。

英文绘本里的最经典的就是《Mr Noisy’s Book of Patterns》，里面发出的声音就是符合规律特征的，click click clack。 

上面这本国内不一定容易买得到，但大家很熟悉的《Chicka Chicka Boom Boom》这本也是符合规律的绘本。

无处不在的规律

而生活中也是有很多规律存在的。

路上捡的树枝和树叶

水果摆盘原来也是规律

苏斯博士的这本《Oh, the place you go》，想想上面的图案规律，我们的衣服或者妈妈的丝巾上有没有呢？

“跨界”延展是我们经常容易忽视的，但非常重要，涉及到孩子的观察和短期记忆能力，也锻炼了认知灵活性。

这样的思路适用于所有早教启蒙，当孩子掌握了某个新概念，不要着急往前进，先停一停，看看能否往旁边拓展。

广度的拓展，看上去是“浪费时间”，但这样孩子的思维就能灵活，这就是“举一反三”的知识迁移能力。

规律的再延展

这些基础打扎实后，接下来就是规律的再延展。

光是发现理解规律不是目的，任何思维模式都是为了解决实际问题。那么同样的，规律也是需要回归到“解决问题”能力上。

这里继续举例，大家可以根据我的例子进行举一反三。

解题方法是什么？先画出这些规律，然后数一数就有答案了。

这个举例，也是让大家可以理解，低幼孩子解决问题的方式是具象思维，就是需要拿个实物搭一下，或者画出来，然后找到答案。

这也是为什么我从不鼓励大家提前教孩子背公式这类的计算，具象思维没得到良好的发展，而抽象思维根本还没到这个年龄，得不偿失。

幼小衔接到底衔接什么？

帮助孩子尽可能多地利用具象思维理解抽象概念，解决抽象问题。

我们以前老话总说，数理化好的人聪明。这句话对也不对，真正严谨的说法是，具有数学思维的人普遍更加聪明。

而传统教育中，我们经常把数学启蒙简单视为计算启蒙，从而错过了非常宝贵的数学思维启蒙的阶段。

我想，这才是天才儿童班启蒙对我们普通家庭来说，最有价值的借鉴意义吧。

转载声明：本文仅代表转载平台的观点，如有异议，请以医生意见为主。