感觉好久没写数学启蒙了，倒不是忘记了，而是数学是我曾经的短板和痛楚，所以沉寂了一段时间，自己在学习和实践。

我的学习模式一定是需要看“全局”，然后再“深入”。不然很容易就变成了“三分钟热度”，折腾自己和孩子，学会了从0数到100就完事了。

那么今天就先和大家分享一个全局观，也就是学龄前必须掌握的五大数学能力。

文末有个小投票，关于这五大能力，大家希望了解更多的是哪个，那么接下来再和大家仔细深入地聊。

数数

虽然叫“数数”，其实更加准确的是数感（数字感觉）。

认识并且可以读出来肯定是第一步，这是唱数。可以顺着数，也可以倒着数，这是唱数的进阶版。

而数感不仅仅止于这里，还有很多活学活用。最简单的是，可以一一对应数物体，并且明白数完的最后一个数字，就是这群物品的总数（基数）。

第二步可以理解序数，也就是“第一、第二”这些概念。

然后可以进行进阶，非常熟练地明白某个数的前后数字，可以根据一定规则跳着数（比如隔5、隔10数）。

这时，对于10个以内的物体，可以做到看一眼直接说出多少，而不再需要一个一个数出来了。

可见，学龄前的数数启蒙，并不是比拼孩子可以从1数到10，还是从1数到100，而是有没有真正把数字用活了。

空间

空间关系，有两个关键的概念：图形和空间。

第一步是理解图形，可以认识大部分常见的2D图形。

第二步是可以把大大小小不同的图形进行归类，这就说明了孩子内在建立了对于图形属性的理解。

第三步就是可以描述图形。分享一个我和小D曾经的对话：

当时小D的这个回答就说明了，她其实并没有真正扎实掌握三角形这个概念。

那么顺着她的答案，我就可以提供下面这些图形，继续问：这些都是三角形吗？

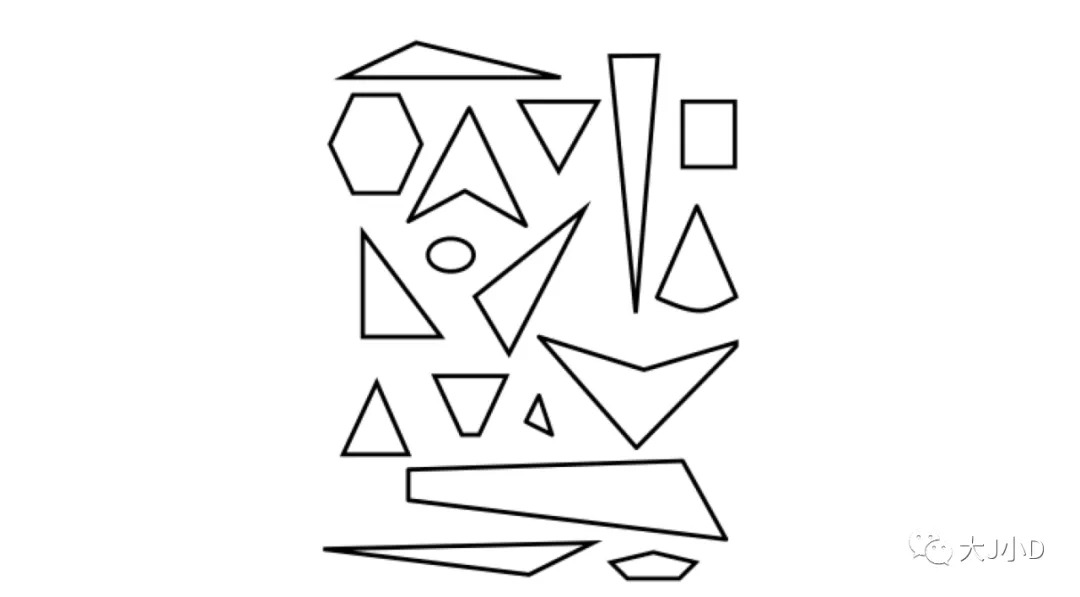
那为什么不是三角形呢？哦，原来并不是所有尖的都是三角形，三角形需要有三条边和三个角。

之后就可以逐渐引入3D图形了，昨天正好有人问到：

其实这个并不需要担忧，孩子认识形状就是从2D开始的，当他们可以真正掌握了上面提到的平面形状要求，那就可以尝试引入立体的。

最简单的方法就是给孩子一个三角形一个立方体，问问他，有什么区别？学习方式和上面分享的2D学习是类似的。

空间关系的第二个概念是空间，第一步就是了解方位词，常见的有“里面、外面、前面、后面、下面、上面”。大部分孩子掌握“左右”会更慢一点。

第二步是使用方位词，最开始是在自己身上演示，比如“把手放在自己头上”，慢慢可以摆放其他物体，比如，“把小熊放到电视机后面”。

最后是空间转换能力，也就是不用使用具体物体，而是在脑海里就能完成某个形状转移的样子。

这个是学龄前最高阶的空间能力的培养。

拼图、一些类似七巧板、魔方的玩具都是可以很好锻炼这方面能力的。

如果你观察就会发现，不少孩子一开始玩七巧板都是“试错“方式，就是毫无目的地这里放放，那里放放，其实说明他们还没有建立空间转换。

慢慢开始摸到门道了，这种随意性就会减少，这就说明了他们开始在脑中进行“空间转换”了。

这是我们最近宅家弄的一个乐高魔方，我昨晚刚刚录了视频，北京时间这周六晚上和大家分享哦～

等式

字面意思上一提到“等式”，估计大家第一反应就是，要教计算了。其实并不是的，学龄前的“等式”启蒙，就是能够明白等式背后的意义。

第一步就是学会比较，5比4，是大还是小？我有3颗糖，你有2颗糖，谁有更多的糖？

第二步就是可以引入加减的早期启蒙，你有2颗糖，妈妈再给你1颗，你有几颗。

最后一步，才是把这些加减游戏变成等式公式。

让孩子明白例如“+、-、=”这些运算符号的含义，就是我们日常对话里的“多给你”、“拿掉”、“一共”的意思。

有这些作为基础了，才是接下来的10以内加减法。但也绝对没必要“超纲“要求孩子不断操练学会的。

运算能力再快，未来也是拼不过人工智能的，但是如何拆解等式，如何把公式进行演算，这才是数学思维的体现。

举个例子，“凑10法”。6+8等于多少？

这些粗看觉得很慢，但这些才是真正数学思维在起作用，你也能看到，在这个过程中，之前打下基础的“数数”能力就体现了。

规律

规律，意思就是一个序列按照一定规则不断重复出现。

第一步是根据实物进行，最简单的就是ABAB规律。比如“红黄红黄红黄”。一开始孩子只要认出这是规律就好了。

然后可以预测规律，比如给了“红黄红黄”，可以知道接下来也是“红黄”。

最后就是自己可以创造新序列，比如“葡萄苹果葡萄苹果”。

第二步是复杂规律，比如AABAAB、ABAABA，类似这样的，同样也可以按照上面的进行。

然后就需要有所延展，不仅仅是颜色，不仅仅是物体，还可以是语言，也可以是动作，还可以是数字。

一般来说，数字是最难的，因为最抽象，所以前面关于规律的基础打的越扎实就越好。

数字规律，一开始也可以从简单进入，比如“11223344”，再逐渐过渡到更难的，比如“2468”、“5、10、15”等。

不少人应该都听过规律是早期数学启蒙的一部分，但也许并不是所有人都能理解这和数学有啥关系。

我之前就是不理解的，学了以后才明白，这是代数的雏形。

但最关键的是形成“代数思维”，而不是会运算代数。

所谓代数思维，就是可以从一系列的事物中去发现他们的共性，并且通过这些共性的提炼，来解决问题。

听上去挺抽象的，但想想生活中那些善于“举一反三”的人，其实就是具有“代数思维”的。

测量

测量的基础需要前面提到的，已经有了大小、多少这些比较概念和数字思维能力。

早期的测量不需要使用测量工具，更多的是对于数据的理解和运用，需要解决这样三个问题。

第一，明白数量指代关系，比如桌子有三辆车那么长，但有五块积木那么长。

第二，理解“公平比较”概念，比如我和爸爸谁高，大家都必须站在地面上比较，不能是我站在桌上和爸爸比，这是今后关于数据起始点的概念。

第三，理解“相对”概念，比如，桌子的“三辆车”和“五块积木”，虽然数字有差别，但他们是一样长的，只不过指代数量不同。

这里强调的测量，不是会不会测量，还是那句话，使用工具这些技能，以后很容易会被取代，真正关键的是这些思考过程。

小D想用手掌测量恐龙的高度

今天谈的这五大能力，每一个都值得深挖和拓展，那么就想请大家投票，哪个是你们最想先了解的？

我知道大家肯定希望选全部，所以我特地设置了单选题，也能帮助我了解大家最迫切的“知识短板”。

我也知道，有一部分朋友看完会觉得很晕，那想想当年你所不熟悉的语言启蒙、社交启蒙等等，其实也是这样的学习过程。

只要大家有学习热情，那么我就会一如既往，把数学启蒙板块一点一点写出来，并且仍然做到有实操，在家就能做。

最后，也想和大家说几句掏心窝，我对数字不敏感，从小偏科严重。这也是为什么，进修早期儿童教育时，这么晚才选择上数学启蒙的课程，自己畏难了。

但真正钻进去后，我反而觉得数学很有趣的，并不是我传统意义理解的计算几何，真的是生活中处处都有数学，尤其是在低幼孩子启蒙的阶段。

这也是为什么，我今天特别希望可以给大家一个全局观，让大家发现，我们曾经学习时那么难的内容，其实就是缺少了学龄前“有趣”的体验。

我蛮遗憾自己小时候没有这么“玩”数学，那么接下来，就让我们带着孩子一起“玩转”数学吧。

转载声明：本文仅代表转载平台的观点，如有异议，请以医生意见为主。